Copyright Andrew Suter: Used with his permission.
The real world is Analogue, "Relating to or using signals or information represented by a continuously variable physical quantity such as spatial position, voltage, etc." Not only is the value continuously variable, but it has a value at every instant in time.
When we represent the real world inside a computer it becomes a digitised version and is no longer continuously variable in value and only has a defined value at discrete instants in time.
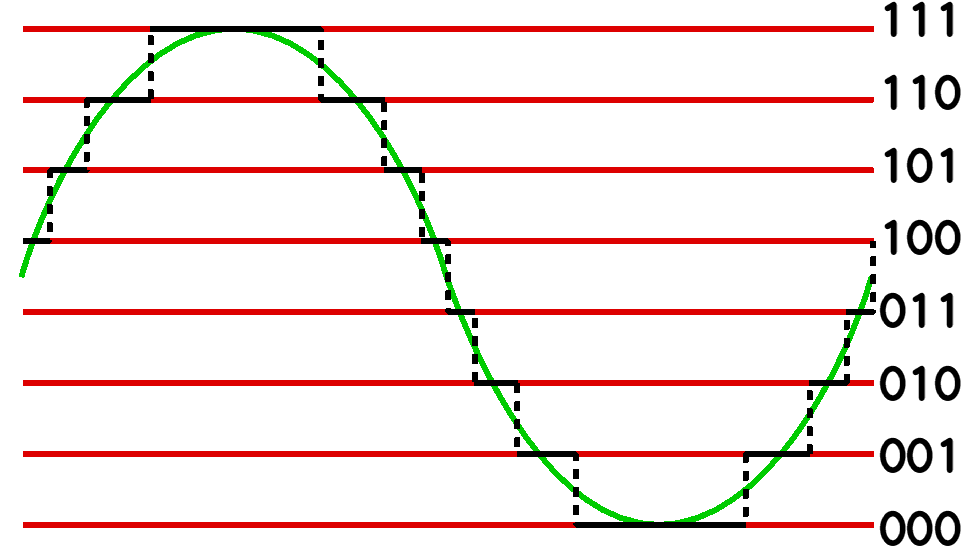
On a piece of graph paper we draw an analogue signal with a continuous line but a digital signal is more like a series of dots that can only be drawn on the intersections of the vertical and horizontal lines.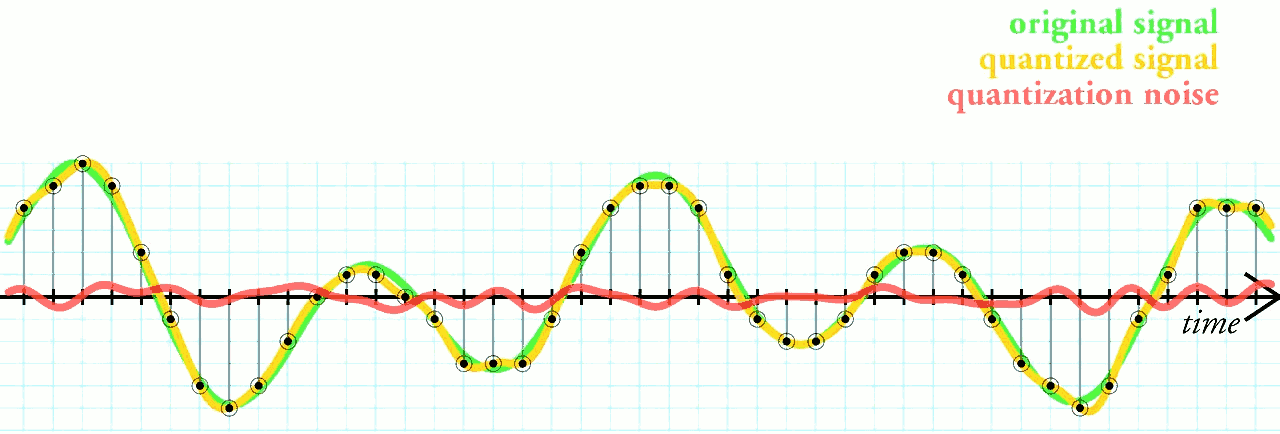
How close the dots can be is determined by the "resolution". On the time (x) axis this is set by the sampling rate, on the y axis it is set by the number of bits in the variables used to represent the each value. It's just the same as the resolution of your monitor or TV set. A "1920x1080" screen gives a more detailed picture that an "1024x768" display. It also takes more information to produce a higher resolution picture.
If we consider digital sound, a typical sampling rate is 44100 samples/second as used on CDs, though on PCs 48000 samples/second is more common. Sound samples are typically represented as 16 bit numbers which gives 65536 possible values, though the use of 24 bits for samples is increasing.
Just as a higher resolution monitor gives a clearer, more detailed image, higher sampling rates and more bits per sample increase the clarity of recorded sound. In particular the sampling rate determines the highest frequency that will be included in the digitised version of the signal.
The diagram below shows how a smooth (analogue) waveform is quantised into the 8 possible values representable in a 3 bit variable. The difference between the true value and the quantised version is called the "quantisation noise" and is represented by the red line in the previous diagram.

Introducing noise to a signal is generally something to be avoided, but quantisation noise can be reduced by simply increasing the resolution of the analogue to digital conversion and using more bits to hold the digital values.
An example of "Time Quantisation" is the production and projection of a film. When first invented they were called "Moving picture" (hence the term "movies") but they are in fact made up from a series of static snap shots or single frames. When these are projected in sequence the audiences' eyes and brains fill in the gaps between the frames and the viewers see smooth motion of the objects on the screen.
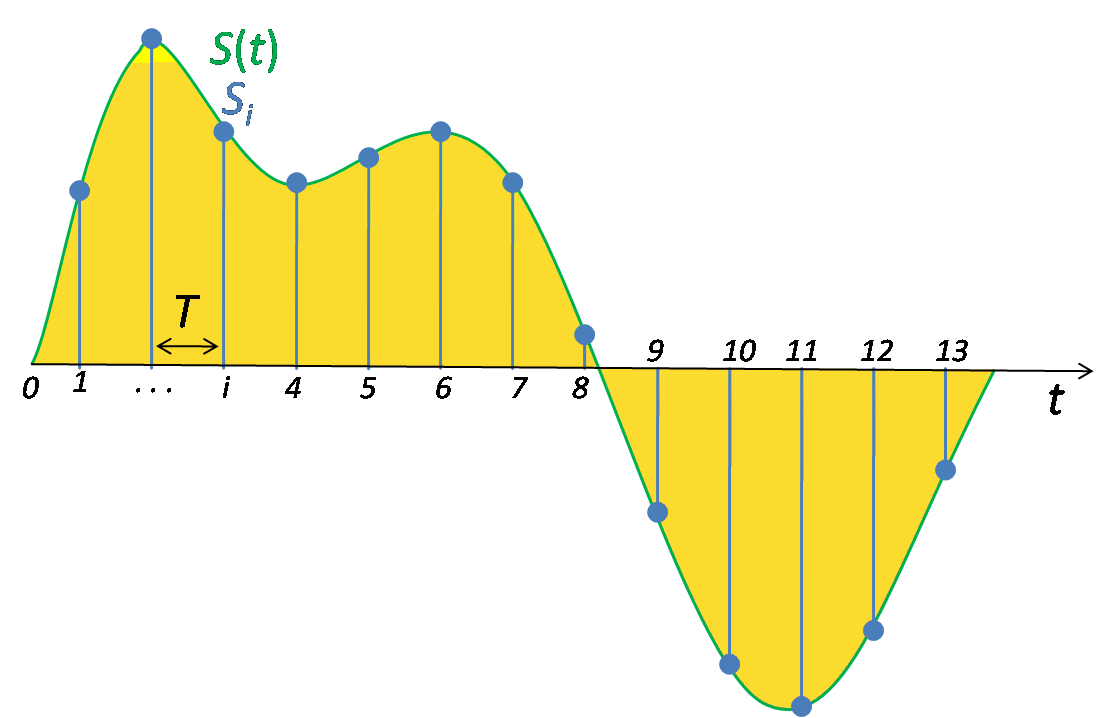
The diagram below shows a continuous signal (green line) that has been sampled to produce values at only discreet times (blue dots). Only time quantisation hs been applied so the blue dots can be at any height.
There is a potential problem with sampling. The sampling rate determines the highest frequencies in the original signal that are correctly preserved in the sampled version.
If a sound signal is sampled 48000 times a second, only frequencies up to 24kHz will be correctly preserved in the sampled version. Actually care needs to be taken to ensure that there are no frequencies above 24kHz
in the original signal.
This has two practical consequences. A signal containing frequencies upto F hz either
The diagram below shows two signals (red and dotted lines) which both produce the same samples (black dots). The frequency of the dotted line signal is below Nyquist frequency but the frequency of the red line signal is above it.
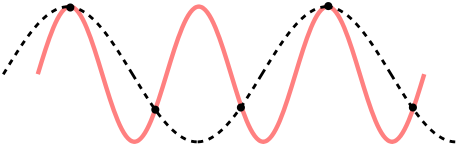
This is the same effect that causes the wheels on wagon in old western films to sometimes appear to be turning backwards ! It is called "aliasing", and a filter designed to remove frequencies above the Nyquist frequency are called "anti-aliasing filter".
The French mathematician and physicist Joseph Fourier discovered that repeating wave forms (such as the signal produced by a steady note from a musical instrument) can be broken down into a set of simpler sinusoidal wave forms. For a steady note these are termed the harmonics and have frequencies that are multiples of the original note. So a steady 880Hz note on a violin is composed of harmonics at 1760Hz,2640Hz,3520Hz etc. The process that finds these frequencies and their strengths is called Fourier Analysis.
The reverse process to Fourier Analysis is Fourier Synthesis. The diagram below shows how a square waveform can be synthesised by adding together a series of sine waves.
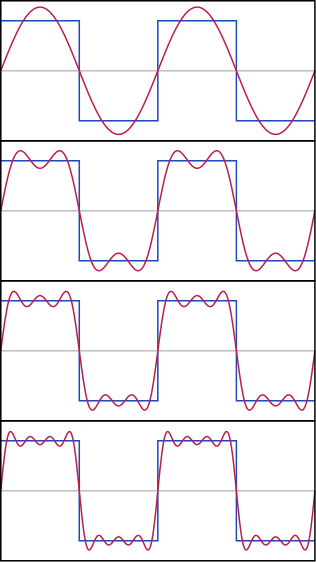
Only the harmonics are present in a square wave, and their strength follow a simple 1/n relationship:
| Harmonic | Frequency | Amplitude |
| 1st | 1000Hz | 1 |
| 3rd | 3000Hz | 0.333 |
| 5th | 5000Hz | 0.2 |
| 7th | 7000Hz | 0.143 |
The next animated diagram shows the relationship between a time domain graph (where the x axis is time) and a frequency domain graph (where the x axis is frequency).)
.gif)
Luckily you don't need to understand the details of the mathematics of the Fourier Transform to understand what it does!
As originally conceived Fourier Analysis dealt with continuously varying waveforms and involved the evaluation of lots of integrals. The "Fourier Transform for the digital age" is called the Discreet Fourier Transform (DFT) as it deals with sampled waveforms and uses series summations rather than integrals. Luckily there is hardware in modern computers that is especially well suited to evaluating summations! The Fast Fourier Transform is an efficient implementation of the DFT.
The FFT uses various short-cuts to speed up the calculations, and these can only be used when transforming a waveform that has been sampled into 2N samples. You may have see references to 256-point FFTs or 2048-point FFTs.
Earlier I stressed the importance of a "steady" waveform when considering Fourier Analysis. In absolute theoretical terms this means that the waveform has been going on forever and will never stop. In practical terms it means that single cycle of the waveform can be identified. For an FFT to produce the best results it is necessary to sample a waveform at a rate such that a integer number of cycles exactly occupies 2N samples. Since this implies the sampling rate should change depending on the frequency of the signal being sampled, and since most systems use fixed sampling rates, it follows that FFTs do not in general produce the best results possible.
An FFT performs a (Discreet) Fourier Analysis on the input data. The result of the transform has the same number of values in it as the input data, so transforming 1024 samples of a signal produces 1024 values in the transformed version. [That's not quite true but it's good enough to be going on with for now.] In the case where a single cycle of the input signal exactly fills 2N samples, then the values in the output correspond to the strengths of the harmonics present in the input samples. [Note that at this stage I'm ignoring the concept of "phase"]
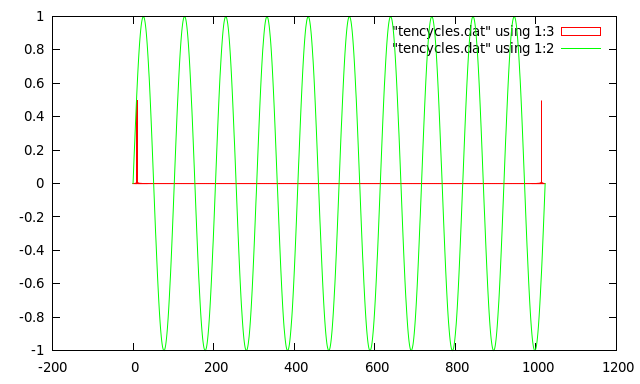
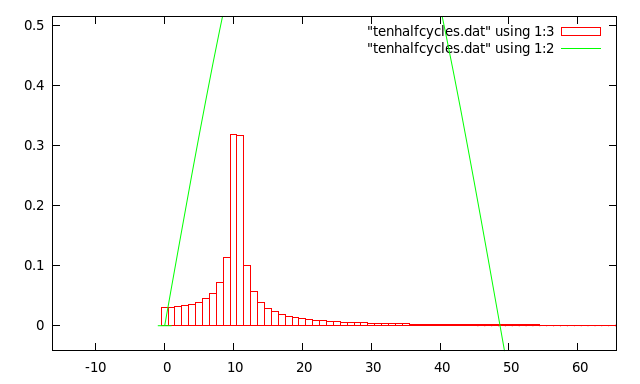
Here is an example where the numbers are arranged to make the explanation simple....If we apply an FFT to our 1024 sample buffer containing 10 complete cycles of a sine wave, then the result will look like the diagram below. The green line shows the 10 cycles of sine wave that exactly fit into 1024 samples, and the red line shows the result of applying a FFT to the sample. The transformed data has non-zero values in the 10th and 1014th buckets .
You will recall that sampling a signal restricts the frequencies that are correctly preserved in the sampled version, and the "anti-aliasing filters" are used to remove signals above the Nyquist frequency. For example, sampling at 48000 samples/second only correctly preserves frequencies below 24000Hz (24kHz). However, in the example above I said that the 1024 FFT result buckets covered the range 0Hz to 48000hz. This would imply that result buckets 512 to 1023 shoud be empty, but the diagram below shows this is not the case.
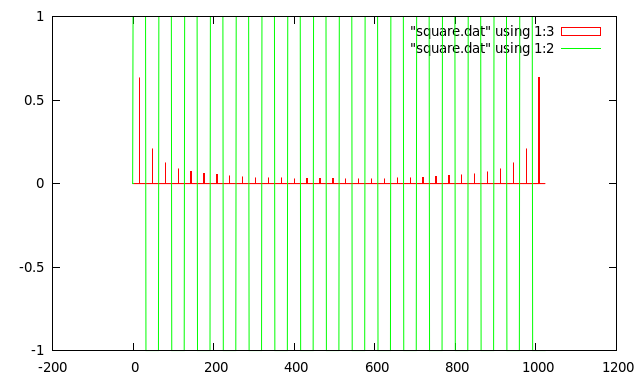
In fact the second half of the transform result contains a mirror image of the first half. This is more clearly shown in the next example which shows the FFT result for a sampled square wave which fits 16 cycles exactly into 1024 samples.
Zooming in shows that the square wave is made up of frequencies at odd multiples (harmonics) of 16, and that they get weaker as they increase in frequency.

Note: The description above has been simplified to bring out the most important features. See the section below on "Complex data sources" for a more complete description.
In reality waveforms never fit exactly into 2N samples. Here's a simple example of a sine wave that has been sampled so that 10.5 cycles fit into 1024 samples:
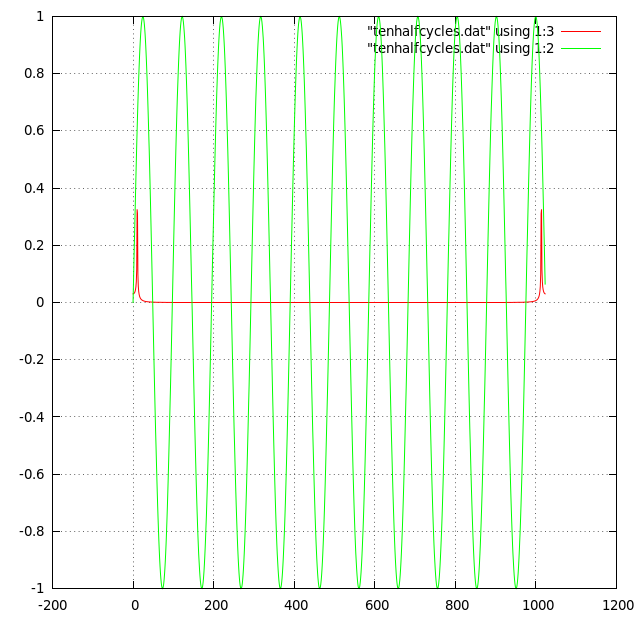
A zoomed in version shows each bar representing the value in each frequency bucket.
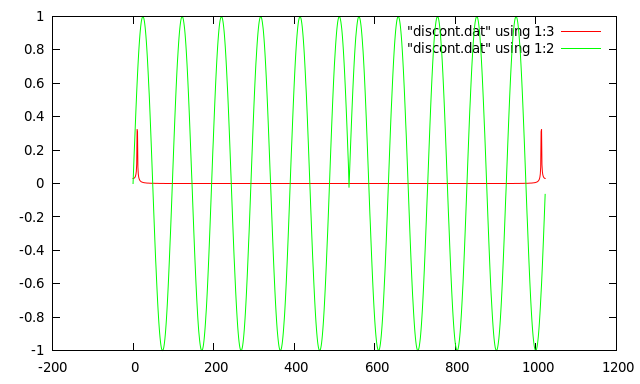
As far as the FFT is concerned the signal is repeated (forever) to the left and right of the 1024 samples. This means there is a discontinuity in the waveform every 10.5 cycles.
Here is the same waveform shifted in time to put the periodic discontinuity in the middle of the graph.
You can see that he discontinuity has caused the sharp peak in the transform to be smeared out over several frequency values. This is called Spectral leakage.
A square wave that doesn't quite exactly fit into 2N samples suffers spectral leakage around each of its harmonics:
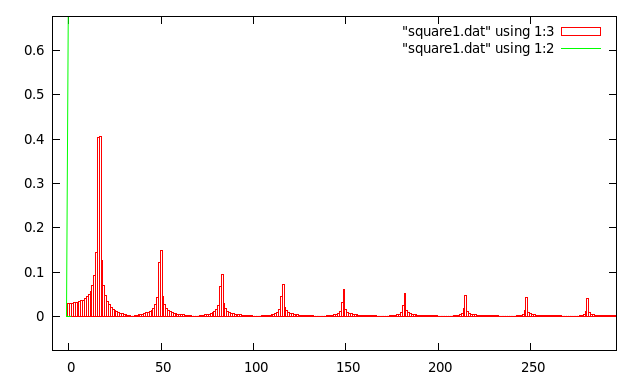
It is the waveform discontinuities caused when the beginning and end of the input data do not join up perfectly that creates Spectral Leaking. So if the ends could be made to join up smoothly the problem could be eliminated. This is what was happening in the "ideal data" cases shown above. A simple answer might be to just ignore the data near the beginning and end of the array, but just setting the first and last few samples to be zero would just create more discontinuities ! But the basic idea is usable and is called "windowing"
First of all here what windowing does to the ideal 10 cycle sine wave used in the previous section:
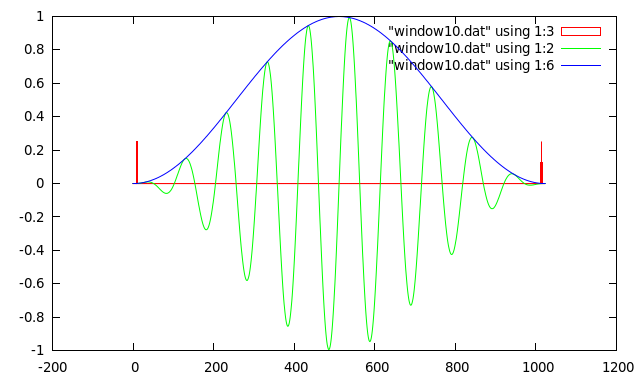
The blue curve shows the windowing function that has been used to shape the sampled data. This particular windowing function is called a Hanning window. BUT since we have changed the input to the FFT we must expect the output to have changed as well. The next diagram shows the transform of the ideal 10 cycle sine wave with the window applied:
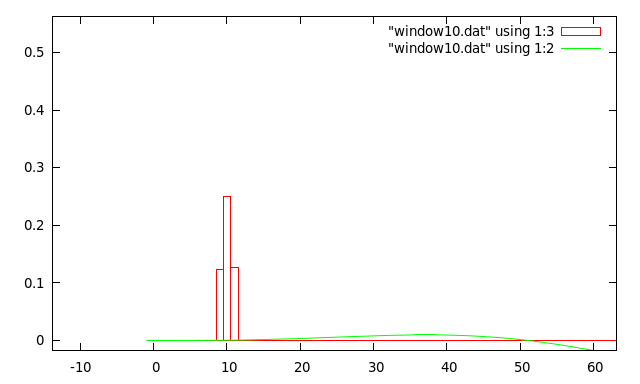
It can be seen that windowing the ideal data has itself produced some spectral leakage. So the question is "has it improved the transform of real world data ?" For ease of comparison here is the transform of the 10.5 cycle sine wave again:

And here is the transform of the same data with the window applied:
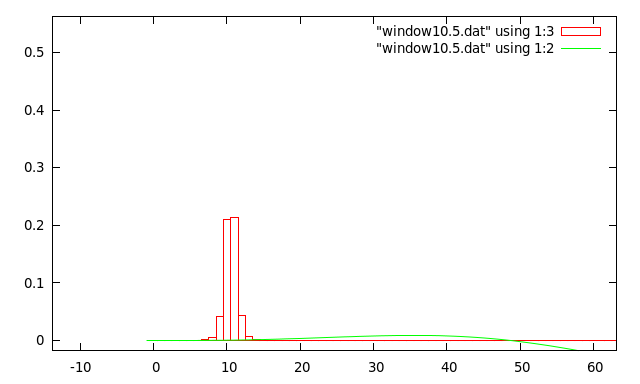
It is clear that the spectral leakage has been greatly reduced, but so that the overall amplitude of the transform result. This particular Hanning window has a "gain" of 0.5.
Here is the transform obtained by windowing the square wave that didn't quite exactly fit into 2N samples:
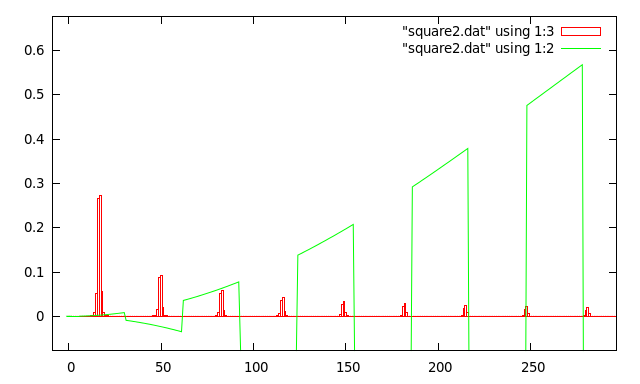
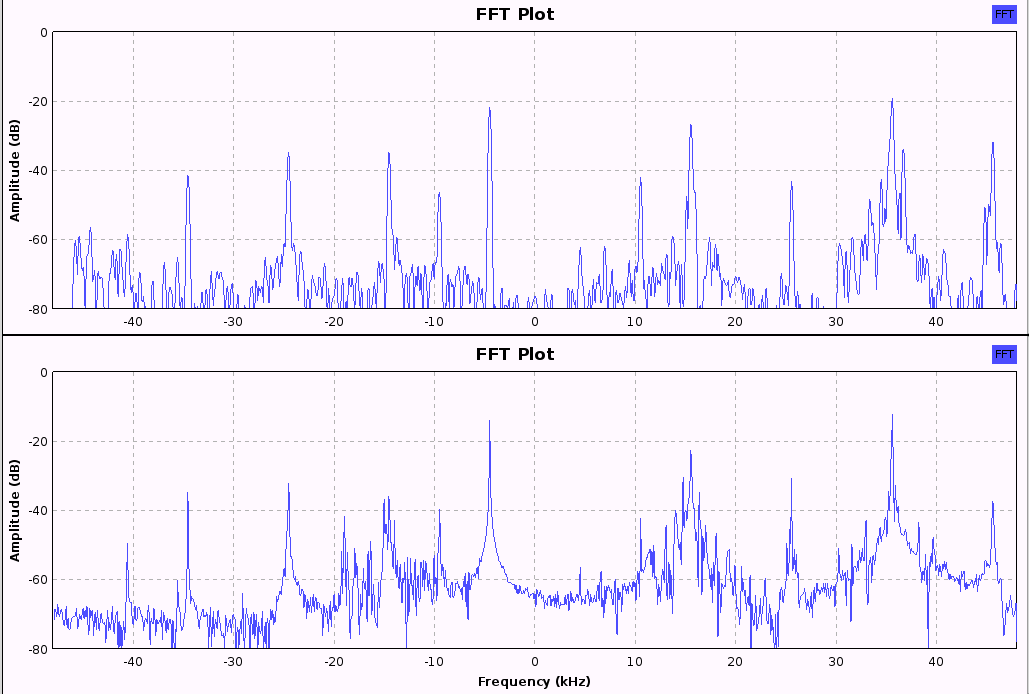
And finally, here are a couple of plots of the FFTs of some real world signals. The input signals are taken from the Shortwave Radio "41 meter band". The center frequency is 7.270Mhz, and the signals were sampled at 96kHz. The first pair of graphs show FFT results first with and then without the use of a windowing function. The peaks correspond to the "carrier wave" for each station at -35,-25,-15,-10,-5,+10,+15,+25,+35 and +45kHz. The peaks are much more clearly defined in the top graph, and the effects of frequency leakage can be clearly seen in the bottom graph.
The next diagram shows the "waterfall" displays for the same signals. These have time on the vertical axis and show the amplitude of signals at each frequency using brightness. This time the non-windowed version is shown first
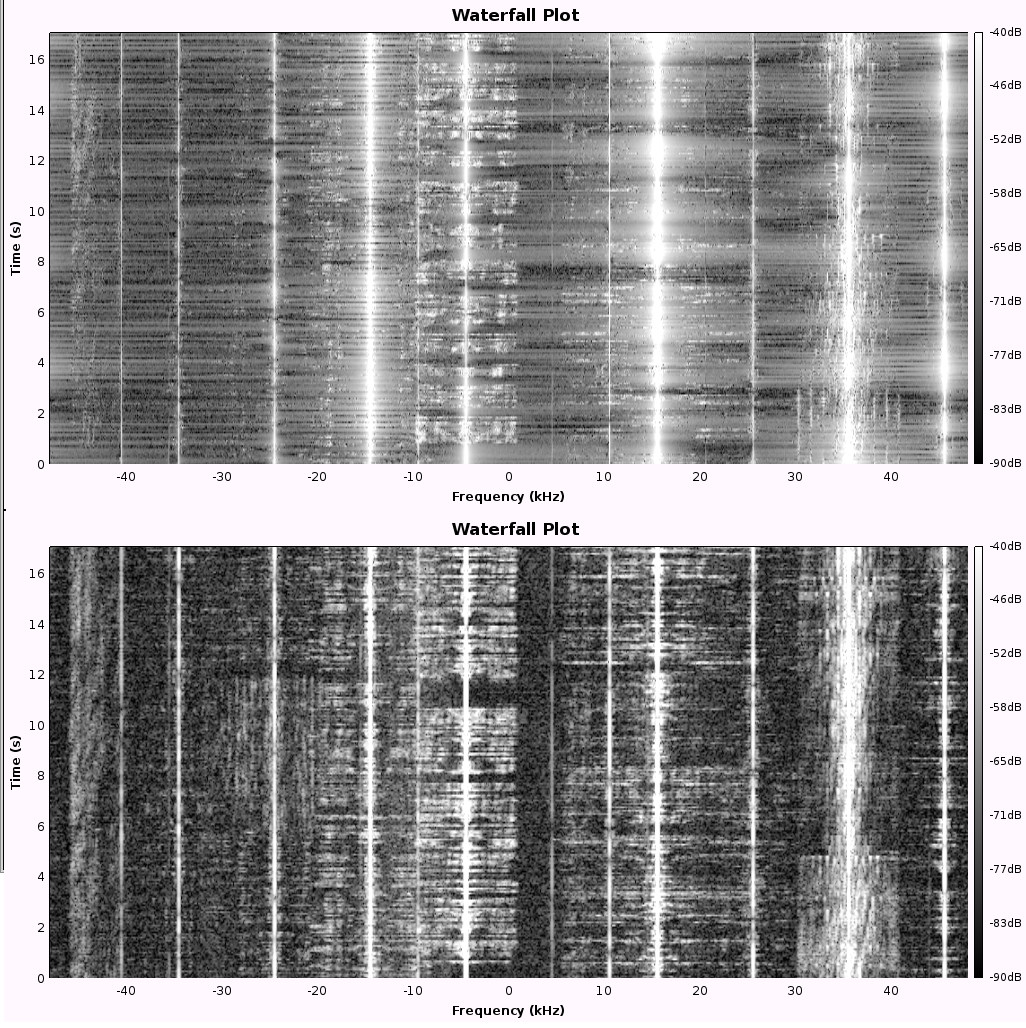
The above images were produced using "GNU Radio Companion" and an Elecraft KX3 radio.
See the "complex signal sources" section for an explanation of how 96kHz sampling has been able to produce 96kHz of spectrum display.
Another side effect is that when performing a set of transforms on a series of buffers, it is possible that short bursts of high frequencies could be almost totally missing from the transform output if they occurred around the transition between buffers.
First of all there are a few things to note about the example code found in /opt/vc/src/hello_pi/hello_fft
The API is really very simple. There are only four function calls and two data types to understand. However there is some use of 'C' pointers, which is a language feature that I know gives trouble to some programmers. But don't worry, I'll give plenty of explanation where appropriate.
This is just a simple wrapper structure for a pair of floats that form a complex number. This is not the place for a in depth explanation of complex number theory, so if you want ot know more I suggest you spend a few moments with GOGGLE. The real and imaginary parts are held in structure members "re" and "im".
This is an semi-opaque structure that holds all the information about the transform setup. There are three members of importance to the programmer:
int mbox_oopen(void);
This needs to be called once before any of the other functions as it establishes communications between your program and the gpu. It returns a file handle (int) that needs to be passed as the first parameter in the "prepare" function described below.
int gpu_fft_prepare(
int mb, // mailbox file_descriptor returned by calling mbox_open()
int log2_N, // Size of the FFT data is 2log2_N so a value of 12 configures the gpu to transform 212=4069 samples
int direction, // use GPU_FFT_FWD to perform the forward (time to frequency domain) transform and use GPU_FFT_REV to perform the inverse (frequency to time domain) transform
int jobs, // number of transforms to perform in "batch mode". Set to 1 to just perform one transform.
struct GPU_FFT **fft // A pointer to a pointer to a GPU_FFT structure (see below for more explanation)
);
The parameter named "fft" is a pointer to a pointer hence the "**" in its declaration. The actual structure of type "struct GPU_FFT" will be created within the gpu_fft_prepare function
but its address needs to be returned to our code so that it can be used later. So within our code we need to have a pointer variable that points at a struct GPU_FFT. Our code passes the
address of this pointer variable into the gpu_fft_prepare function which then puts the address of the sturct GPU_FFT into our pointer variable.
All of the memory associated with the FFT input and output data is allocated within gpu_fft_prepare.
A typical call might be
gpu_fft_prepare(mbox,12,GPU_FFT_FWD,1,&fftinfo);where fftinfo has been declared as
struct GPU_FFT *fftinfo;If only a single transform is required this code sequence could be used...
struct GPU_FFT_COMPLEX *dataIn,*dataOut; struct GPU_FFT *fftinfo; gpu_fft_prepare(........,&fftinfo); dataIn = fftinfo->in; dataOut = fftinfo->out;
unsigned gpu_fft_execute(struct GPU_FFT *info);This is the library call that actually gets the gpu to do all the hard work! Notice that it has no references to the input and output data in its parameters as these are contained within the info structure.
void gpu_fft_release(struct GPU_FFT *info);This is a "house keeping" function that should be called at the end of a program. It deallocated the memory and also some internal gpu resouces. To start with your programs will still work without it , but they may start to fail if they are run lots of times which causes the gpu runs out of some of its internal resources. After this call returns the info pointer should be considered to be invalid.
All signal sources are going to include some form of Analogue to Digital (A2D) converter. In some cases the A2D will be proceeded by some analogue filtering to attenuate frequencies above the Nyquist frequency. Some may provide a continuous stream of samples while others may only perform a conversion when commanded to do so. They may be connected via USB,SPI,I2C,I2S or GPIO busses. The most common signal source on PCs is a sound card which provides A2D functions for recording and D2A functions for playback. If you want to use an audio card as your signal source the easiest solution on a RPI is to use a USB connected sound card. These will typically provide 16bit resolution at 48kHz resolution. Some only provide one channel for recording from a microphone.
I've not used any I2C or SPI connected A2Ds myself but if you have details of any that work please let me know and I'll include them here.
This will depend greatly on the type of application. For example if you are recording environmental data such as temperature,sunlight & humidity, then these only change very slowly and can be sampled one or twice a minute. The same goes for wind speed, but if you want to catch any short lived gusts one sample a second may be more appropriate.
A signal from a Seismograph may have components at up to 50Hz present, so in this case at least 100 samples/second would be needed to capture all the important data.
Signals measuring vibrations in rotating machines will depend on the speed the machine's speed. For example the fundamental frequency from a machine turning at 1000 rpm will be 1000/60 = 16.7 Hz
Audio signals from a quality microphone will typically reach up to 20kHz, but for "communications quality" speech signals above ~3kHz can be removed. PC sound cards used to provide a range of sampling rates from 8Khz up to 24kHz, but current devices seem to be limited to 44.1kHz (CD rate) and 48kHz. The lower rates were needed because early PC's CPU's couldn't process the amounts of data produced by higher sampling rates! To get a greater range (= high rates) you need to pay for a better device.
USB devices capable of 96kHz stereo sampling are easy to find, and ones which offer up to 192kHz are available. BUT I've found that currently the USB interface on the RPI is not able to reliably handle 192kHz devices, and until recently couldn't handle 96kHz devices either.
If you are only interested in the analysis of human speech then 48kHz is more than adequate, but if you are after detecting the ultrasonic sounds from bats (for example) then 96kHz or even higher may be needed.
If you are interested in digital communications used on HF radio, then these are typically only a few kHz wide and will appear as audio signals at a radio receivers headphone socket.
Some of the latest amateur radio receivers produce what is known as "I/Q" outputs which may produce signals up to 200kHz. More information about these is in the "Complex data sources" section.
Lets work out an example:
Assume we wish to update our spectrum display 10 times a second. With a sampling rate of 48kHz that means each display update needs to consume 4800 input samples. We could use a 4800 sample buffer and ignore some of the data to allow the use of a 4096 sample FFT. Or if we used a 4096 sample input buffer and 4096 sample FFT we would get 48000/4096 = 11.7 updates/sec.
Due to some of the problems associated with missing short bursts of signals when using widowing, we may decide to perform multiple shorter, overlapping FFTs on each input buffer.
Imagine for a moment that you know which town I live in. If I wanted to invite you to my birthday party, I could tell "I live at number 25, Long Road." Just telling you that "I live at number 25" isn't enough. Likewise "I live on Long Road" isn't enough either, but it would get you close to the party!.
I know you have a GPS in your car, so I could give you the GPS coordinates of my house instead of the street name and number. Or I could give you the GPS coordinates for the end of the street and also give the house number.
If I had given you my full address, then when you arrived at my party you could press the "save" button on your GPS and it would store the GPS coordinates of my house so that you could find your way back after making a trip to the nearest supermarket because you forgot to bring any beer :-)
"Long Road" is like an array of houses. The house number tells you how many houses to pass to get to my house (assuming you start from the right end of the street!), but the GPS coordinate allow you to find my house without even knowing which town my street it is in , of how far down the street I live.
If we used 'C' like syntax for house addresses we might write addresses like this : Long Road[25]
In a 'C' programme we declare arrays like this:
type arrayName[size];so assuming we had a suitable type defined for a house, a declaration for my street would look like this
House MyStreet[150];To access my house we could write
MyStreet[25];
A 'C' pointer is like GPS coordianates, it allows access to variables in arrays without knowing the array name or the index into the array. To declare a "House pointer" variable called "anyHouse" we write
House *anyHouse;To set anyHouse to the equivalent of the correct "GPS coordinates" we use the "address of" operator "&" on a House like this:
anyHouse = &MyStreet[25];which would set anyHouse to point at my house
All the houses in my street are the same size, so if we increment anyHouse it will now point at number 26 (which may be next door or across the street depending on how the house number are arranged). In 'C' arrays element No. 26 is always next to No. 25. (NOTE: Incrementing a House pointer will cause problems when it reaches the last house in the street!)
Now lets look at a definition of a house type
typedef struct house
{
int numberOfBedrooms;
bool hasGarage;
bool lastHouseInStreet; // Needs to be set to true for the last house is each street
} House ;
If we want to know if No. 35 has a garage, we use the structure member operator "." (dot) and write
if(MyStreet[35].hasGarage == true)
{
......
}
If we want to know if the house pointed to by anyHouse has garage, we first have to follow the pointer to the particular house structure before we can test if it has a garage. Following a pointer is called "dereferencing" and uses the "*" (star) operator. So if we write
*anyHousewe get a House. You might think that you could write
*anyHouse.hasGaragein your programme, but the C compiler will object:
error: request for member `hasGarage` in something not a structure or unionThis is due to the relative precedence of the dot and star operators. We need to use
(*anyHouse).hasGarageto get the desired result. Accessing structures' members via pointers is so common that it has its own shorthand operator, "->" . So the example above becomes
anyHouse->hasGarage
To test if a house has a garage we could write
if(anyHouse->hasGarage == true)
{
......
}
The following code counts the number of houses in my street that have 3 or more bedrooms
int houseCounter;
House *aHouse;
houseCounter = 0;
aHouse = &MyStreet[0]; // Convention dictates we have no house "Number zero" :-)
do
{
aHouse++; // Move to the next house (Note how the first time this statement is executed it conveniently skips over House No. zero)
if(aHouse->numberOfBedrooms >=3) houseCounter += 1;
}
while(aHouse->lastHouseInStreet == false);
We've seen how dereferencing a house pointer with "*" produces a house, and how we can use the "&" operator to set a house pointer to point at a particular house in an array of houses. But what is "MyStreet" ? Well it is actually the equivalent of the GPS coordinated of the real street. Thus
MyStreet[25]actually says "Here are the GPS coordinates for the start street, and you need the 25th house. (This means that
MyStreetand
&MyStreet[0]amount to the same thing.)